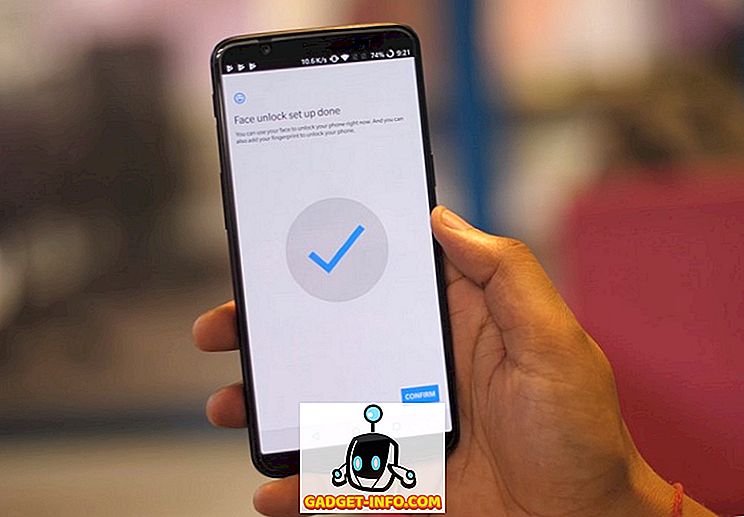
Parametre, popülasyondaki birimlerin ölçümlerinden elde edilir. Buna karşı, istatistik, numunenin elementlerinin ölçümünden alınmıştır.
İstatistik çalışırken, parametre ve istatistik arasındaki fark önemlidir, çünkü bunlar genellikle yanlış anlaşılır.
Karşılaştırma Tablosu
| Karşılaştırma için temel | istatistik | Parametre |
|---|---|---|
| anlam | İstatistik, nüfusun bir kısmını tanımlayan bir ölçüdür. | Parametre, popülasyonu tanımlayan bir ölçümü ifade eder. |
| Sayısal değer | Değişken ve Bilinen | Sabit ve Bilinmeyen |
| İstatistiksel Gösterim | x̄ = Örnek Ortalama | μ = Nüfus ortalaması |
| s = Örnek Standart Sapma | σ = Nüfus Standart Sapması | |
| p̂ = Örnek Oranı | P = Nüfus Oranı | |
| x = Veri Öğeleri | X = Veri Öğeleri | |
| n = Numune büyüklüğü | N = Nüfus Büyüklüğü | |
| r = Korelasyon katsayısı | ρ = Korelasyon katsayısı |
İstatistiğin Tanımı
Bir istatistik, bir veri örneğinden elde edilen sayısal bir değer olarak tanımlanır. Örnek gözlemin tanımlayıcı bir istatistiksel ölçüsü ve işlevidir. Bir örnek, tüm popülasyonu tüm özelliklerinde temsil eden popülasyonun bir kısmı olarak tanımlanmaktadır. İstatistiğin yaygın kullanımı, belirli bir popülasyon parametresini tahmin etmektir.
Verilen popülasyondan, çoklu numuneler çizmek mümkündür ve farklı numunelerden elde edilen sonuç (istatistik) numunelere bağlı olarak değişecektir.
Parametre tanımı
Nüfusun tüm unsurlarını temel alan sabit bir özellik, parametre olarak adlandırılır. Buradaki nüfus, ortak özellikleri paylaşan, incelenmekte olan tüm birimlerin toplamını ifade eder. Nüfusun her bir üyesi parametreyi bilmek için araştırıldığı için değişmeden kalan sayısal bir değerdir. Sayım yapıldıktan sonra elde edilen gerçek değeri gösterir.
İstatistiksel ve Parametre Arasındaki Anahtar Farklılıklar
İstatistik ve parametre arasındaki fark, aşağıdaki gerekçelerle açıkça çizilebilir:
- Bir istatistik, nüfusun küçük bir bölümünün bir özelliğidir, örn. Örnek. Parametre, hedef popülasyonu tanımlayan sabit bir ölçüdür.
- İstatistik, sabit ve bilinmeyen bir sayısal değer iken, popülasyon örneğine bağlı değişken ve bilinen bir sayıdır.
- İstatistiksel gösterimler, aşağıdaki gibi verilen popülasyon parametreleri ve örnek istatistikler için farklıdır:
- Popülasyon parametresinde, µ (Yunanca harf mu) ortalamayı, P, nüfus oranını belirtir, standart sapma σ (Yunanca harf sigma) olarak etiketlenir, varyans σ2 ile gösterilir, popülasyon büyüklüğü N ile gösterilir, ortalamanın standart hatası ile gösterilir. σ x̄, standart orantılı hata σ p, standart değişken (z) (X-) / σ ile gösterilir, varyasyon katsayısı σ / by ile gösterilir.
- Örnek istatistiklerinde, x̄ (x-bar) ortalamayı, p̂ (p-hat) örnekleme oranını, standart sapma s olarak etiketlenir, varyans s2 ile temsil edilir, n örneklem büyüklüğünü belirtir, ortalamanın standart hatası s x̄ ile temsil edilir, standart oran hatası s p, standart değişken (z) (x-x̄) / s ile gösterilir, değişiklik katsayısı s / (x̄) ile gösterilir
örnekleme
- Bir araştırmacı, Hindistan'da 22 yaş ve üstü kadınların ortalama ağırlığını bilmek istiyor. Araştırmacı, ortalama 40 kilogramlık bir örneklemden ortalama 54 kg ağırlık alır.
Çözüm : Belirtilen durumda, istatistikler Hindistan'da 40 kadından oluşan basit bir rasgele örneklemden hesaplanan ortalama 54 kg ağırlıktır, parametre ise 22 yaş ve üzerindeki tüm kadınların ortalama ağırlığıdır. - Bir araştırmacı bir günde erkek gençler tarafından tüketilen ortalama su miktarını tahmin etmek istiyor. 55 erkekten oluşan basit bir rastgele örneklemeden araştırmacı ortalama 1, 5 litre su almaktadır.
Çözüm : Bu soruda, parametre tüm erkek gençler tarafından bir günde tüketilen ortalama su miktarıdır, istatistik ise bir günde 55 erkek basit rastgele örneklemden elde edilen erkek gençler tarafından tüketilen ortalama 1, 5 litre sudur. gençler.
Sonuç
Tartışmayı özetlemek için, popülasyondan elde edilen sonuç, sayısal değerin parametre olarak bilindiğini not etmek önemlidir. Sonuç numuneden elde edilirse, sayısal değere istatistik denir.